반응형
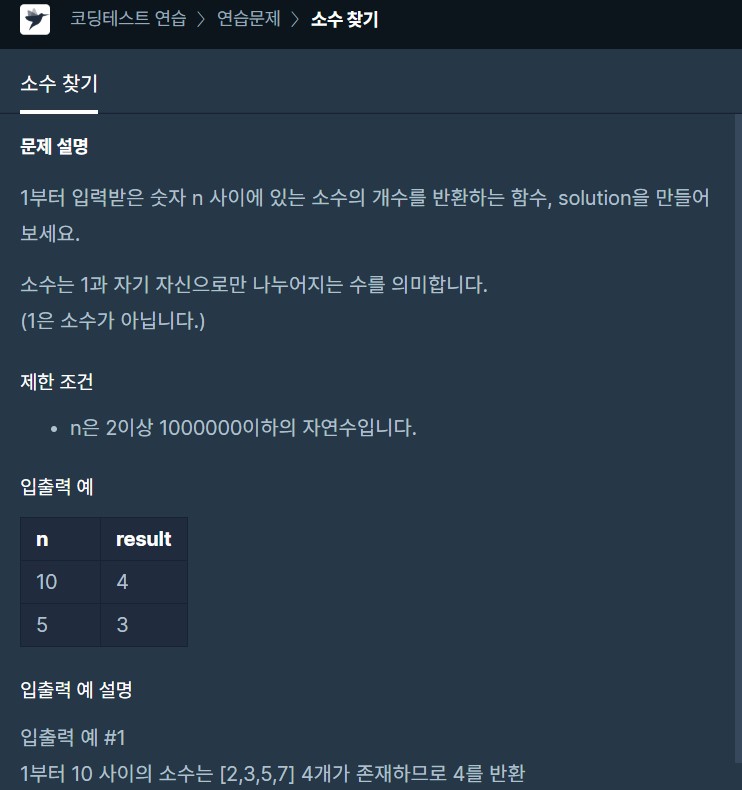
💡 나의 풀이(효율성에서 시간복잡도 큼)
class Solution {
public int solution(int n) {
int answer = 0;
for(int i = 2; i <= n; i++){
boolean chk = true;
for(int j = 2; j*j <= i; j++){ //배수 지우기
if(i % j == 0){
chk = false;
break;
}
}
if(chk){
answer++;
}
}
return answer;
}
}
💡 에라토스테네스의 체를 활용한 소수찾기 코드
(위의 코드보다 실행속도 10배이상 빨라짐 --> Math.sqrt(num) 사용의 중요성)
소수찾기가 의외로 너무 어려워서 다른 사람의 코드를 참고하려고 가져왔다.
class Solution {
public int solution(int n) {
int answer = 0;
boolean[] sosu =new boolean [n+1];
for(int i=2; i<=n ; i++)
sosu[i]=true; //2~n번째수를 true로 초기화
//제곱근 구하기
int root=(int)Math.sqrt(n);
for(int i=2; i<=root; i++){ //2~루트n까지 검사
if(sosu[i]==true){ //i번째의 수가 소수일 때
for(int j=i; i*j<=n; j++) //그 배수들을 다 false로 초기화(배수는 소수가 아니기 때문)
sosu[i*j]=false;
}
}
for(int i =2; i<=n; i++) {
if(sosu[i]==true) //소수의 개수 세기
answer++;
}
return answer;
}
}
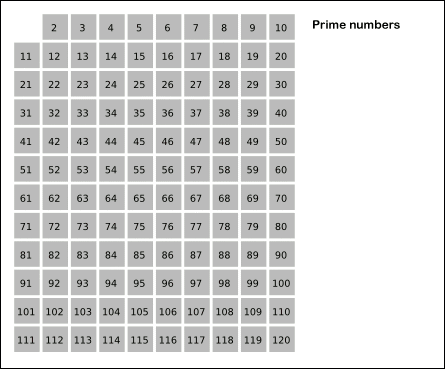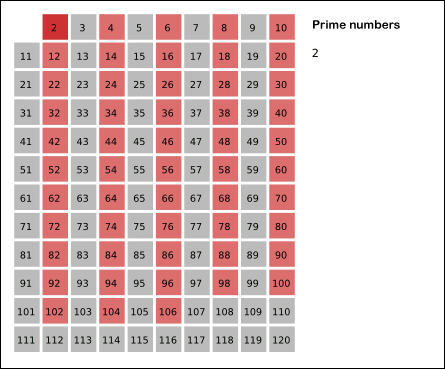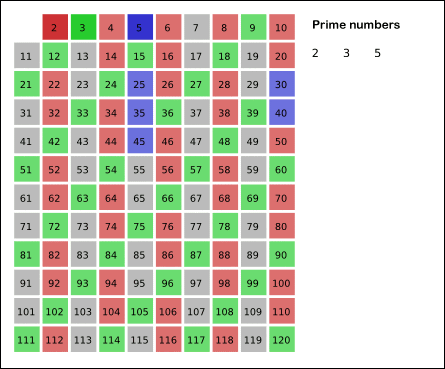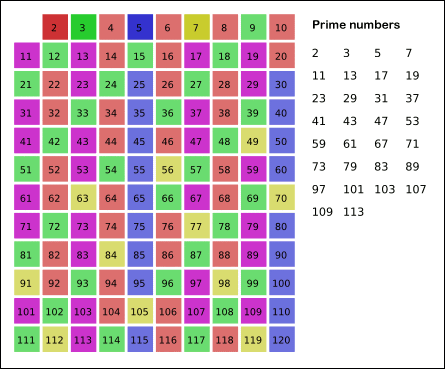
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
반응형
'👩🏻💻 기술면접 > 알고리즘' 카테고리의 다른 글
| [프로그래머스] JAVA 비밀지도(카카오 블라인드) Level 1. (1) | 2020.04.15 |
|---|---|
| [프로그래머스] JAVA 행렬의 덧셈 Level 1. (0) | 2020.04.15 |
| [프로그래머스] Java 문자열 내 마음대로 정렬하기 Level 1 (1) | 2020.04.03 |
| [프로그래머스] Java 나누어 떨어지는 숫자 배열 Level 1 (2) | 2020.04.02 |
| [프로그래머스] Java 모의고사 Level 1 (0) | 2020.04.02 |



